The concept of criticality in living systems is borrowed from physics and refers to a delicate balance where the system operates at the edge between order and chaos. In criticality, small changes can have profound effects, leading to sudden and significant shifts in behavior or function. In biology, there is growing evidence that some living systems may exhibit similar features. For instance, coordinated motion in flocks of birds or schools of fish has been suggested to resemble critical-like dynamics, where even a slight change in the behavior of one bird can cause the entire flock’s pattern to transform dramatically. This critical behavior is not limited to birds; it is present in various biological processes, such as our brains’ neural activity and the beating of our hearts. Contrary to inanimate matter, where criticality is often fine-tuned, living systems appear to be poised near critical points. Scientists believe that this criticality is not just a random occurrence but serves a purpose in living systems. It may optimize information processing, enhance adaptability, and enable living organisms to respond quickly and efficiently to their ever-changing environment. Understanding criticality in living systems could open doors to new insights into health, disease, and the delicate balance that sustains life itself.
References
2022
-
Mean field fracture in disordered solids: Statistics of fluctuations
Hudson Borja da Rocha, and Lev Truskinovsky
Journal of the Mechanics and Physics of Solids, 2022
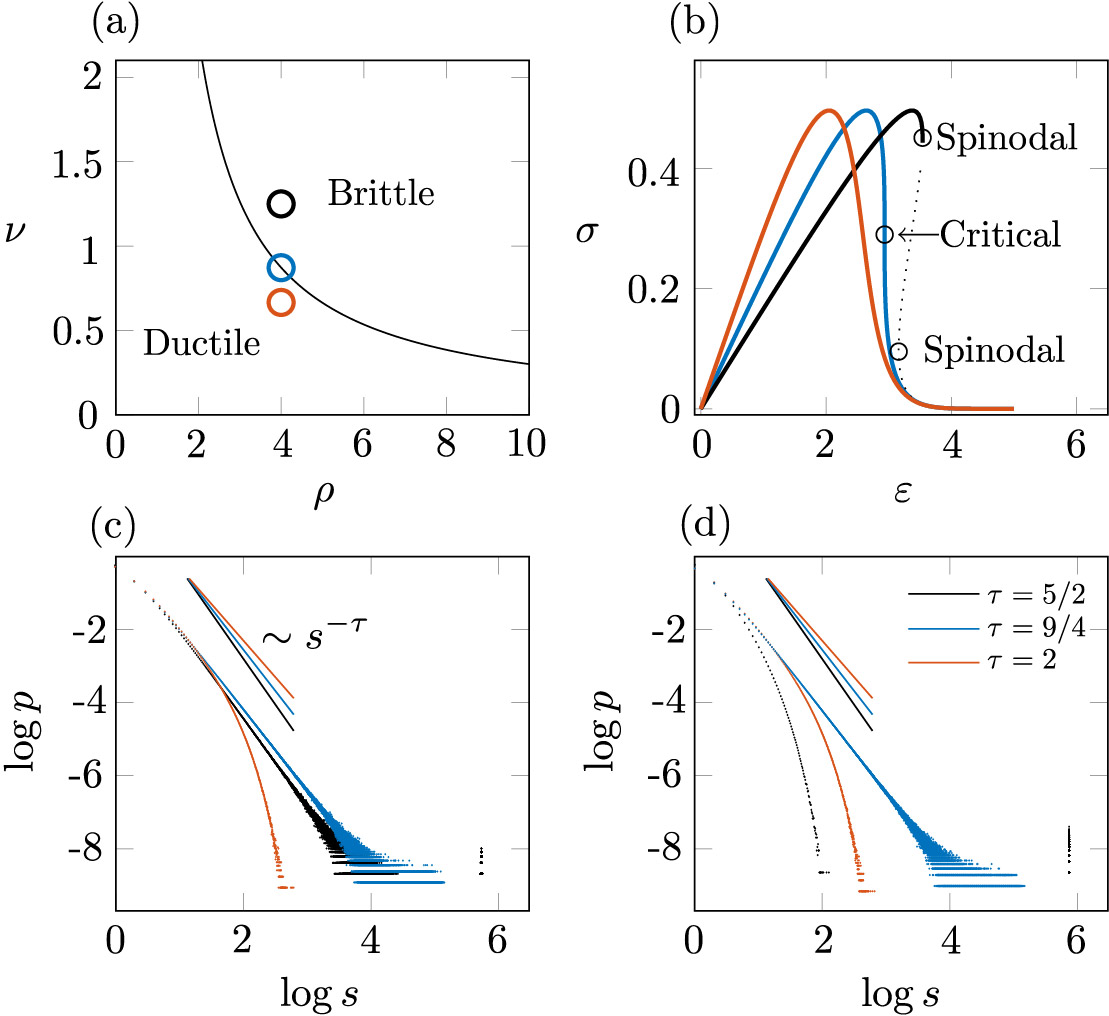
Power law distributed fluctuations are known to accompany terminal failure in disordered brittle solids. The associated intermittent scale-free behavior is of interest from the fundamental point of view as it emerges universally from an intricate interplay of threshold-type nonlinearity, quenched disorder, and long-range interactions. We use the simplest mean-field description of such systems to show that they can be expected to undergo a transition between brittle and quasi-brittle (ductile) responses. While the former is characterized by a power law distribution of avalanches, in the latter, the statistics of avalanches is predominantly Gaussian. The realization of a particular regime depends on the variance of disorder and the effective rigidity represented by a combination of elastic moduli. We argue that the robust criticality, as in the cases of earthquakes and collapsing porous materials, indicates the self-tuning of the system towards the boundary separating brittle and ductile regimes.
2021
-
A plausible mechanism of muscle stabilization in stall conditions
Hudson Borja da Rocha, and Lev Truskinovsky
The European Physical Journal Plus, 2021
2020
-
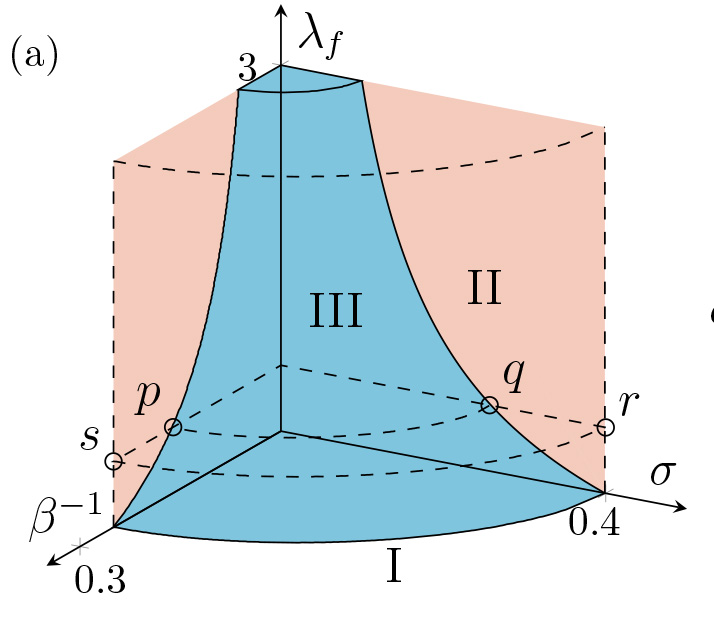
Rigidity-Controlled Crossover: From Spinodal to Critical Failure
Hudson Borja da Rocha, and Lev Truskinovsky
Phys. Rev. Lett., Jan 2020
2019
-
Functionality of Disorder in Muscle Mechanics
Hudson Borja da Rocha, and Lev Truskinovsky
Phys. Rev. Lett., Mar 2019
-
Equilibrium unzipping at finite temperature
Hudson Borja da Rocha, and Lev Truskinovsky
Archive of Applied Mechanics, Mar 2019
We study thermally activated unzipping, which is modeled as a debonding process. The system is modeled as a parallel bundle of elastically interacting breakable units loaded through a series spring. Using equilibrium statistical mechanics, we compute the reversible response of this mechanical system under quasi-static driving. Depending on the stiffness of the series spring, the system exhibits either ductile behavior, characterized by noncooperative debonding, or brittle behavior, with a highly correlated detachment of the whole bundle. We show that the ductile to brittle transition is of the second order and that it can also be controlled by temperature.
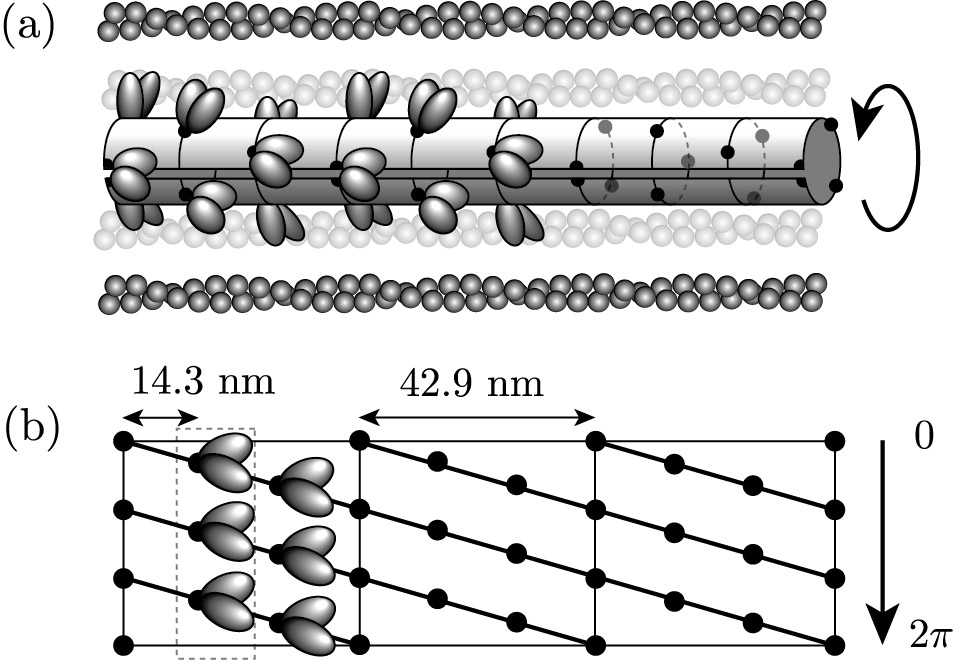 A plausible mechanism of muscle stabilization in stall conditionsThe European Physical Journal Plus, 2021
A plausible mechanism of muscle stabilization in stall conditionsThe European Physical Journal Plus, 2021